Borromean环形签名探究

最近在看grin的介绍，沿着Confidential Transaction了解到Borromean Ring Signature，对于该环形签名是如何设计的比较感兴趣，阅读了论文和介绍CT的文章里也介绍了Borromean环形签名，对于其中一些步骤仍然有些模糊，之后研究了这篇文章作者写的一个python的示例（我看代码时添加了一些注释便于理解，可以参见这里），才明白了当中的设计。由于我也是初入门，哪里有理解错的地方，欢迎与我联系探讨。

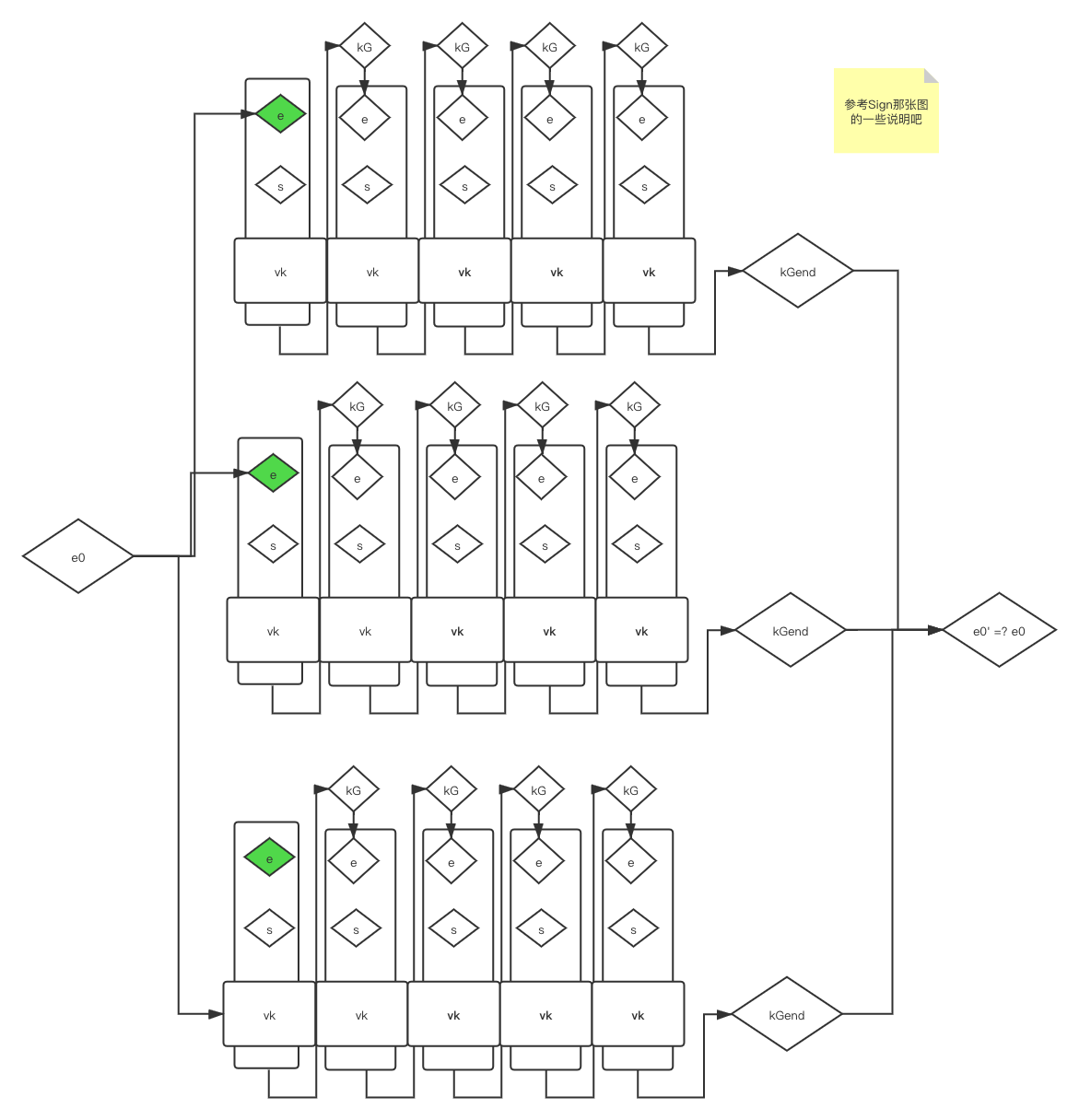
下面是我梳理的整个的流程图，分为签名和验证两个部分:

签名

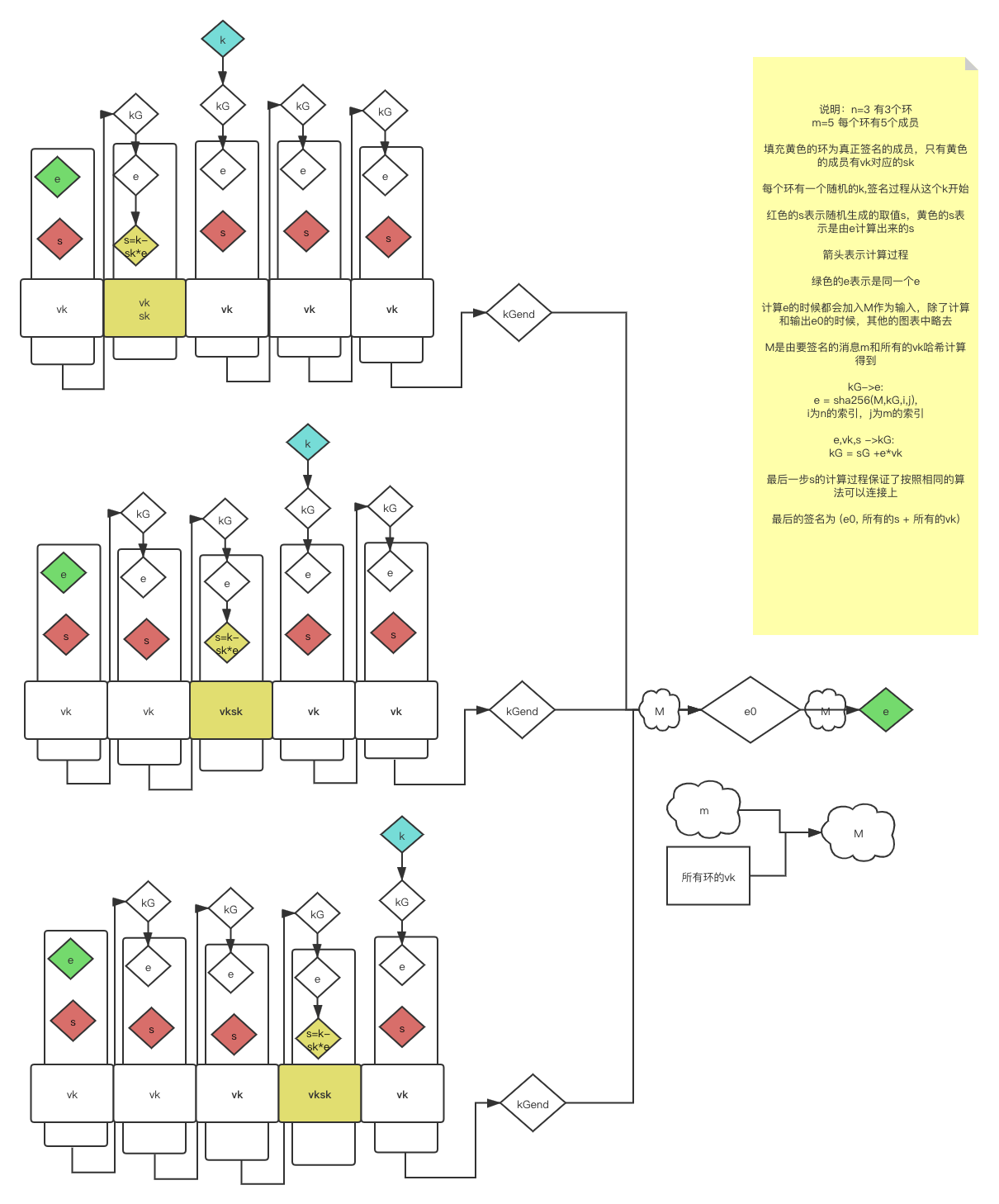
其中根据e,v,s计算kG的方法原文中如下:

def get_kG(e, P, s=None):
    '''Use EC operation: kG = sG +eP.
    If s (signature) is not provided, it is generated
    randomly and returned.
    e - hash value, 32 bytes binary
    P - verification pubkey
    s - 32 bytes binary'''
    if not s:
        s = os.urandom(32)  #随机生成s
    sG = btc.fast_multiply(btc.G, btc.decode(s, 256)) # s*G
    eP = btc.fast_multiply(P, btc.decode(e, 256))     # e*P
    return (btc.fast_add(sG, eP), s)                  # return  kG = sG +eP, And random s

根据kG计算e的方法如下，其中参数pubkey为kG,m为M,i是n个ring里的索引，j是ring里的位置索引：

def borr_hash(m, pubkey, i, j, is_pubkey=True):
    '''A Sha256 hash of data in the standard 'borromean'
    format. Note that 'pubkey' is the value kG as according to
    kG = sG - eP.
    i,j : the indices to a specific vertex in the graph.
    m - the message to be hashed.
    Returns - the hash.
    '''
    # little hack assuming sizes < 256
    p = btc.encode_pubkey(pubkey, 'bin_compressed') if is_pubkey else pubkey
    x = p + m + '\x00' * 3 + chr(i) + '\x00' * 3 + chr(j)
    return sha256(x).digest()

根据要签名的消息m计算M的方法如下，其中vks是所有ring的公钥：

# 这里对应于论文里的 "Compute M as the hash of the message to be signed and the set of verification keys."
def get_sig_message(m, vks):
    '''The full message is a sha256 hash
    of the message string concatenated with the
    compressed binary format of all of the verification keys.'''
    full_message = m
    for loop in vks:
        for p in vks[loop]:
            full_message += btc.encode_pubkey(p, 'bin_compressed')
    return sha256(full_message).digest()

由所有kGend一起计算出e0的方法如下：

to_be_hashed = btc.encode_pubkey(kGend, 'bin_compressed') + ... + M # 所有的kGend相加再加上M

e0 = sha256(to_be_hashed).digest()  # e0 是 每个ring最后一个计算出来的kG加上M计算出来:  sha256(  kG+kG+...+kG  +M)

由e0演算出绿色的e(也就是每个ring第一个e)的方法如下:

e[i][0] = borr_hash(M, e0, i, 0, is_pubkey=False)

验证

验证相比于签名要简单写，从第一个位置开始，根据签名里的e0开始演算，知道最后将所有ring的结果综合起来计算，和e0相比是否相等：

Borromean环形签名探究

签名

验证

END